Encodings and embeddings: How does data get into machine learning systems?

In this series, you've learned a bit about how data is collected for machine learning, but what happens next? You need to turn the collected data -- images, text, video, audio or even just a spreadsheet -- into numbers that can be learned by a model. How does this happen?

TLDR (too long; didn't read)
Complex data like images and text need complex representations if you want to use them to predict or learn
One way to encode this data while preserving information uses linear algebra
Deep learning also uses linear algebra as building blocks for networks and architectures
Word embeddings encoded language into linear algebra structures--enabling deep learning with language
Word embeddings also encode cultural biases and sensitive information

Watch a video summary of this post

Why encode information?

Data is actually encoded all the time! When you save a file, when you open a program, when you write an email and hit send -- all of these take formats humans can interpret and translate them into formats computers can read, write and process.

The default computer encoding is bytes (collections of bits) -- which the computer can store or process using available hardware, like a CPU and attached memory. Bytes are also used to build datagrams which can be used by internet protocols to send data. These same principles relate to how information is also encoded into other messaging standards, like radio waves that are captured via an antenna and then decoded back into audio via a demodulator.

Encoding and decoding require the design and incorporation of standards to ensure systems interoperate properly. Imagine if your email provider took your text and encoded it incorrectly. The receiver of your email wouldn't be able to open it properly.

In the early days of machine learning, encoding and decoding usually involved taking numerical datasets to predict another number, making the encoding, decoding and computation obvious and in some ways unnecessary because the computer already could do math on numbers. For example, if you wanted to project a line or trend based on previous data, you can do that without machine learning. As interest, research and use cases expanded, machine learning approaches reached domains where the data wasn't already encoded in numbers that could be learned easily. There needed to be a way to encode and decode letters, words, images, audio and so on.¹

The "magic" of linear algebra

In some machine learning problems, a simple algorithm works well and quickly outperforms more complex models -- like when modeling simple linear or easy classification problems. In this case, choosing a simple model, a non-learning based algorithm and just using statistical measurements works well.

However, there are many problems where the dimensionality of the inputs are too complex for a simple model. This was the case for computer vision problems, like photo classification and object recognition, until the creation of AlexNet in 2011. AlexNet utilized neural networks and encoded the image into multi-dimensional matrices, or sets of numbers. The encoding mechanism did this in such a way that it attempted to preserve information and relationships and represent those in the resulting matrices. You can think of these matrices as a related set of numbers that preserves the patterns by creating numerical relationships between different "areas" or sections of the encoded data. This is what the machine learning model should learn.

AlexNet was one of the breakthrough image recognition models which introduced deep learning models as viable solutions to the variety of machine learning for image tasks that were common at the time. This was because AlexNet cleverly leveraged a larger, "deeper" neural network architecture (deep learning) than other neural networks at the time. It also used a clever encoding mechanism

Another idea that AlexNet borrowed from earlier computer vision neural networks like LeNet-5 from 1998 was the convolutional layer. These layers require many matrix computations, making them compute-hungry and therefore both computationally and energy expensive. One clever idea from the paper was to parallelize the processing by using two GPUs. In the past usually only one CPU or GPU was used. By parallelizing the computations, the researchers were able to increase the model parameter size and also unlock the power of matrices and linear algebra for deep learning.

In the following diagram from the original paper, each of the dotted lines and rectangles inside a layer show an example of what computations run at each layer on the parallel GPUs. You can think of each layer as a series of linear algebra matrix computations that take the results of the previous layer and continue to compute with them, with the goal of optimizing for the learning task at hand. You will learn about these in more depth in a later article.

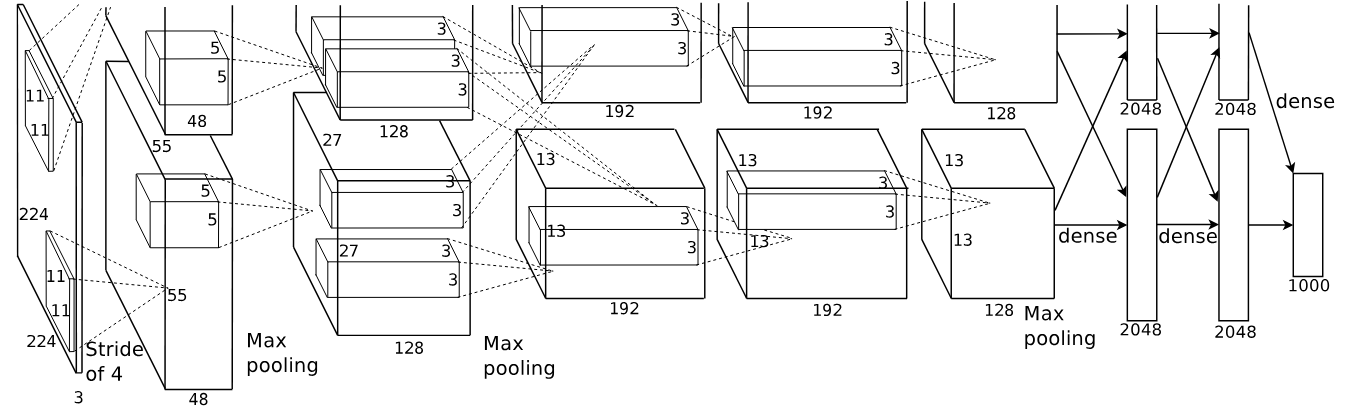AlexNet Architecture Diagram

Linear algebra has been used for hundreds of years to build systems of equations and map them to linear spaces. What does that mean and why is it relevant? You can take real world problems in engineering or physics and model them in mathematics. By taking data or known properties and building it into a system of equations and then mapping those equations into a "space", you essentially compress the problem space and can create optimized ways to solve for all results or a set of optimal results. You can also use these modeled systems to predict, infer, observe and learn.

Linear algebra powers many machine learning systems and is the core building block of deep learning. By modeling complex tasks like how to locate and name the objects in an image (image segmentation and object detection/recognition) in linear algebra systems, deep learning can perform these quite challenging tasks.

Computer vision benefited greatly from encoding images into matrices and leveraging those to unlock linear algebra powers, but what about text? Let's explore the changes that allowed for language-based deep learning, or natural language processing (NLP).

Encoding language with tokens and embeddings

Natural language processing leverages learnings from the field of linguistics. One way to encode language is to use linguistic knowledge like language families and root words to chunk text into smaller words or stems. You do this to achieve smaller and more consistent building blocks of language so that you can concentrate on patterns or information contained in a smaller vocabulary. In NLP, these linguistic chunks are called tokens. For example, you might take the word "foundation" and "founding" and "found" and agree that they should all be reduced to "found". This works fairly well, but what about the "found" in "lost and found"? Does it have the same meaning? The beautiful complexities of language and how each language develops differently adds challenges to tokenization.

There are many approaches to tokenization, or the breaking down of text into machine learning ready chunks, which become quite language specific. Some of the approaches to tokenization include word-roots or stems, like the example above. Another approach is reading a language character-by-character, which works well for languages where one character has a lot of meaning, like Chinese. The character-based approach also works well when trying to do machine learning with less common languages, where there might be many words that aren't represented well in the training data. For character-based tokenization that the word found becomes literally a list of letters: "f", "o", "u", "n", "d". As you might imagine, this doesn't preserve as much of the deeper meanings of the word, because it doesn't necessarily attempt to find things like word roots explicitly -- although the machine learning model can still learn patterns of certain character sequences.

There are also in-between approaches like subword tokenization, where linguistic understanding is used to break each word into word parts or pieces. This works well because it doesn't reduce the information as much as doing word-based tokenization with word stems. For example, "foundation" might become two tokens: "found", "ation" instead of being reduced to just "found". Hugging Face's introduction to tokenization is a great read to learn more in-depth about how different tokenizers work.

Why are there so many approaches to tokenization for NLP? Due to the long-tail distributions you learned about in the previous article, many languages are underrepresented in the online content available when compared with English. In addition, there are niche topics and content compared to more popular content.

These imbalanced data problems present issues when encoding tokens into numerical representations so you can successfully train machine learning models. Early techniques borrowed from linguistic concepts like token frequency or tried to build encodings based on interesting uncommon tokens. These techniques didn’t successfully encode the relationship of the words to one another in longer texts or passages. These encoding methods and the related datasets presented challenges for early natural language processing models because they had to deal with extremely sparse datasets. Imagine choosing a number for every possible token and then just saying whether the token is there in a sentence or not. You will end up with many tokens that are missing in each sentence. This made machine learning difficult and costly because computing on sparse data is harder for computers to do.

An important moment in text- and language-based machine learning was the creation of word- or token-embeddings, which moved away from sparse matrices and allowed for better leveraging of linear algebra (and therefore deep learning). In 2013, Word2Vec (short for word to vector) was released. Word2Vec is a machine learning model which takes a word or token and maps it to a vector representation which is learned by first training the model on the linguistic relationships in text. The vector is like an encoded version of the word which tries to map its relationship to all the other words that the model has processed.² This process produces mathematical connections or links between the words which show up together frequently, and it also can map different relationships when the word is used in different contexts, like the "found" example earlier in this article. This is why these representations are called "word embeddings", borrowing from the mathematical concept of embeddings.

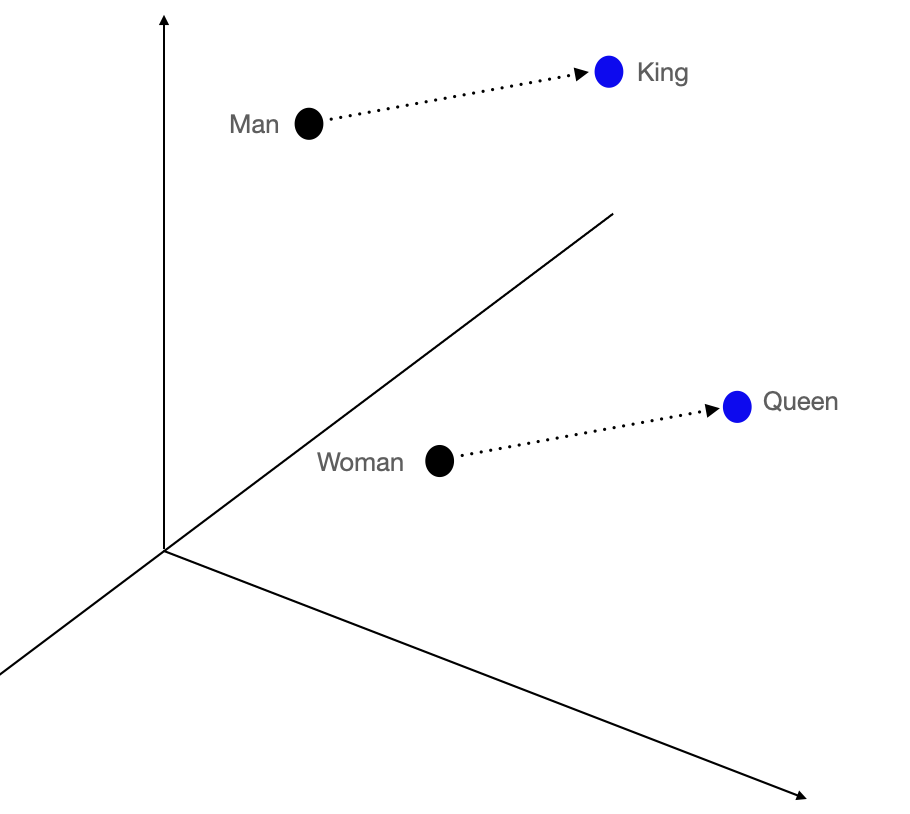Simplified 3D space example of Word2Vec word embeddings and their relationships

Word2Vec introduced a context-aware way to link words in embedded form to one another. The Word2Vec model acted as an encoder into a compressed linear algebra space that translated the linguistic relationships more accurately. One famous example from the original paper used the model used to complete analogies, like Man is to Woman as King is to Queen. When you took the vector representing "man" and subtracted that for "woman", you got a resulting vector showing the distance and direction between those two vectors. If you took this difference and applied it to "king", you got "queen". Pretty neat!

Unfortunately, these embeddings had many other issues, including my discovery shortly after Google released their Word2Vec model that Man is to Computer Programmer as Woman is to Homemaker. 🙄 The resulting embedding models had learned racism, homophobia and US-centricity, which you can read more about it via research by Bolukbasi et al. and Garg et al..

There are many newer approaches than Word2Vec, but the underlying principles remain similar. To learn about the advances that happened or to dive deeper into the topic, check out Vicki Boyles's fantastic and freely available exploration of embeddings.

In the context of deep learning memorization, maybe it might be useful than to memorize some relationships between these tokens. It can be quite useful to know that certain words always appear together, or that certain names are inherently connected. But this brings up considerations for privacy. Should embeddings related to private individuals be able to be learned or memorized?

Do embeddings contain personal information?

In Summer 2024 the Hamburg data protection authority released a discussion paper stating that LLMs do not contain personal information. While the paper is not a legal ruling, it does set guidance for companies within Germany (and presumably the EU) who have interest in using, fine-tuning or training LLMs. For organizations who provide services in the EU, and therefore must follow the EU General Data Protection Regulation (GDPR), these opinions provide useful legal interpretation and guide compliance and privacy decisions.

Let's take a concrete example from the paper. The paper uses the question (in German): Ist ein LLM personenbezogen? (English: Is a LLM personal [data]?) which the paper tokenizes like so:

[I][st][ e][in][ LL][M] [ person][en][be][z][ogen] [?]

The paper also uses the example of someone named Mia Müller, stating that Mia's name is tokenized as "M", "ia", "Mü" and "ller". This is a key example used to say that the name is now split into tokens, and is therefore no longer personally identifiable.

They reference OpenAI's tokenizer, which has a handy online interface, so let's check their work quickly:

GPT-3 Tokenizer

GPT-3.5 and GPT-4 Tokenizer

Using GPT-3, I can reproduce their experiment... but there are differences between GPT 3 and 3.5. How come?

OpenAI's tokenization uses byte-pair encoding which helps for tokenizing multiple languages at once and processing messy internet or chat text. This encoding mechanism uses clever ways to detect and deduplicate linguistic patterns without explicitly incorporating linguistic knowledge.³ To note: the tokenizer doesn't show the embeddings, which are only available via a separate API call (the model is not released publicly for download). The tokenizer takes text and returns a series of indices (like a lookup table) for the appropriate token embedding in the OpenAI system.

When evaluating the GPT tokenization output above, understand that it shows both the tokenizer and the related embeddings for that model. The GPT-3 tokenizer and its trained embedding model produce something closer to character-based embeddings when given German text (and likely this applies to other languages for that tokenizer-embedding combination). The GPT-3.5+ tokenizer and embedding model outputs something closer to subwords.

One possible explanation on the differences between these tokenizer and embedding model combinations is that OpenAI acquired better German language training data, which resulted in better tokenization and embeddings for German text. As shown above, Mia's name is now tokenized as one token per name, meaning those words were common enough to each get their own token and related embedding. In the GPT-3 tokenizer and embedding model, common English names with only one common spelling are tokenized as one name per token.

Therefore, it is misleading to interpret the tokenization itself as a practice that removes personally identifiable data, which is what Hamburg has stated in their discussion paper. If you truly want to have a tokenizer obfuscate personal data, this must be done intentionally and likely is only truly accurate if the identifiable information is never tokenized.

Furthermore, the office incorrectly describes the process of turning tokens into embeddings as an encoding mechanism that further diminishes the "personally identifiable" part of the data. That would be like saying storing a text on your computer makes it not personally identifiable, because it's actually stored in bytes.... which, of course, is not a very useful interpretation of how computer- or machine-readable encodings work. Just because a human cannot look at an embedding and know what word, token or letter it represents doesn't mean that that same person cannot use OpenAI's freely provided decoder to understand what the data is -- or that a machine cannot learn or interpret the data. In fact, this is exactly what machine learning is trying to accomplish.

By default, embedding models like Word2Vec and more powerful ones like OpenAI's model want to retain and internally represent the relationships between tokens. The trained model should take information in the tokens and transfer that into relationships in the embeddings. This learns relationships, like how "be" and "zogen" together is a common mapping, especially if these words follow "personen". This is what makes embeddings so powerful.

In addition, these embeddings are then used to train the actual language model. Nearly all natural language models (deep or otherwise) use embedding sequences to learn patterns. Even if the individual embeddings for a name are chunked oddly due to the tokenization strategy, it's likely that the embedding model has seen their sequence and combination. Even if that embedding model never saw those tokens together as part of the embedding model training, the sequence and relationship between those embeddings can be learned by the language model. By design, tokenization and the embedding model should enhance the ability for the language model to learn the relationships, not detract from it. This feature of data encoding and its subsequent model training means models also learn patterns in personal information.

The interpretation that a model "only sees the multidimensional representation, devoid of personal data" is again, like arguing that a computer processing data only sees bytes, and therefore cannot interpret or that an algorithm cannot learn from personal data. Additionally, the growth of so-called "context windows" means that an LLM or other generative model holds thousands of tokens as accessible data and as sequencing information before creating a response or performing another task. When you chat with ChatGPT, it holds the entire conversation you are having along with the initial instructions or prompt written by the model designers, saving up to 128,000 tokens as additional "context". These embeddings and their ordering can contain many examples of personally identifiable text and are used by the model alongside additional user and session information to formulate a response.

Large machine learning systems attempt to extract and compress information into data structures that leverage linear algebra and deep learning architectures. In doing so, they enable more complex machine learning tasks. This encoding should enhance learning from the data, not detract. Therefore, Hamburg's take is fairly misinformed when it comes to interpreting how personal data (or really any data) is encoded and used in larger machine learning systems.

As you learned in this article, language and computer vision machine learning encode data differently based on the different learnings of how to best leverage the power of deep learning and linear algebra. You might be wondering if computer vision models retain personal information? Some computer vision tasks are set up so the entire goal is to learn personally identifiable information, like with facial recognition systems which should remember the user's face (FaceID as one example). Other tasks might be set up differently, where the model is penalized for learning the specifics. Some questions to ask yourself for further reflection: Should it be known that a photo contains a celebrity, and should that celebrity's name be learned? Should it be learned that a piece of art comes from a particular artist by name? Each of these questions can also be applied to language learning, if a token (or series thereof) ends up representing a person.

In the next article, you'll investigate how machine learning systems take these encodings or embeddings as input and process them for training machine learning models. You'll learn about how machine learning models are evaluated and validated. Finally, you'll explore machine learning culture to see how it affects memorization in machine learning.

I'm very open to feedback (positive, neutral or critical), questions (there are no stupid questions!) and creative re-use of this content. If you have any of those, please share it with me! This helps keep me inspired and writing. :)

Acknowledgements: I would like to thank Vicki Boykis, Damien Desfontaines and Yann Dupis for their feedback, corrections and thoughts on this series. Their input greatly contributed to improvements in my thinking and writing. Any mistakes, typos, inaccuracies or controversial opinions are my own.