Differential Privacy as a Counterexample to AI/ML Memorization
Posted on Do 02 Januar 2025 in ml-memorization
At this point in reading the article series on AI/ML memorization you might be wondering, how did the field get so far without addressing the memorization problem? How did seminal papers like Zhang et al's Understanding Deep Learning Requires Rethinking Generalization not fundamentally change machine learning research? And maybe, is there any research on actually addressing the problem of memorization?
I have an answer for the last question! In this article, you'll explore how differential privacy research both exposes memorization in deep learning networks and presents ways to address these issues.
Prefer to learn by video? This post is summarized on Probably Private's YouTube.
In case differential privacy is new to you, let's walk through how differential privacy works and why it's a great fit for studying memorization.
Differential Privacy: A primer
In 2006, Microsoft researcher Cynthia Dwork released a paper challenging common ideas around releasing data. To note, these ideas were already circulating in her research and related research for several years, but were not yet concretized for data release. In her paper Differential Privacy, she posited that there was no real way to release data without potentially exposing someone's private information if the released information was combined with available external information. For example, if you release the average height of women in Lithuania and someone knows that a woman is 2cm over the average height, that person's height can now be calculated.
This fact that any kind of information release can be detrimental to privacy is obviously at odds with the work of data science and study of information. Dwork and her peers didn't want or intend to stop all research - quite the contrary. They wanted to find new ways to provide safer guarantees than the current status quo, which often just aggregated data and suppressed or removed outliers.
Differential privacy provided a new, safer way to release and share information. Differential privacy is a rigorous and scientific way of measuring information release and its impact on individual privacy. Instead of guessing and hoping you are releasing data in a safe manner, differential privacy gives you a way to measure the data release's impact on individual privacy. When used correctly, it provides strong privacy guarantees for people in the dataset.
Differential privacy does this by giving you a new way to analyze information gain that someone can get by looking at the data. This information gain for the attacker (i.e. person trying to learn more about someone) is privacy loss for the person or people they are trying to expose. The original differential privacy definition prohibits anyone from learning anything too specific about a certain person.
The definition is as follows:
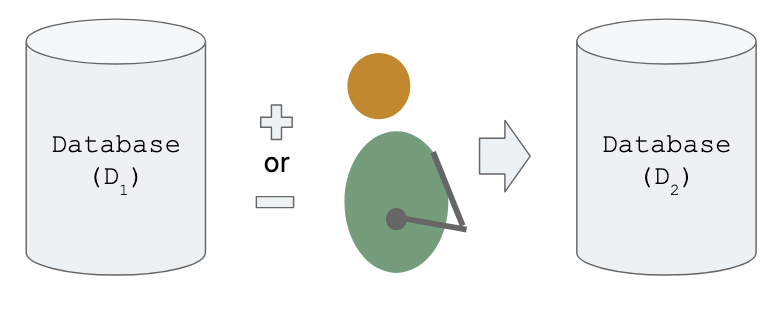
If you don't like math, just read on! It's okay :)
There are two databases (D1 and D2), which differ by one person. The definition tells us that if you ask a question about either database, you shouldn't be able to guess accurately if it is database 1 or 2 based on the answer. If you want to protect the privacy of single persons, you shouldn't notice when the database has changed by only one.
The above equation can be described as a probability bounds problem. However, in this case, instead of reducing uncertainty, you are trying to increase uncertainty. You want the interactions with the database(s) to leak very little information, so the attacker's probability distributions based on prior knowledge and then updated with the information from the query response are closely bound. The attacker should remain unsure about which database they have queried and therefore also unsure about whether the person is in the dataset or not.
Let's take another concrete example to review differential privacy with a real-world lens. Imagine you work at a company with a lot of business dashboards. One of the business dashboards you have access to shows the overall payroll spend by city and role.
You find out someone new is joining the company in your city and you know their role. You're curious about what they are getting paid, so... you decide to take a screenshot the week before they start. Then, you take another screenshot the week they start (or when payroll goes out). When you compare those two screenshots, you have a pretty good guess at their annual salary, presuming they were the only joiner in that specific role/city combination. Even if they weren't the only joiner, you now have a bounds or range of possible salaries, and can better guess their salary.
 Image from my video course on Practical Data Privacy from O'Reilly Learning
Image from my video course on Practical Data Privacy from O'Reilly Learning
This demonstrates the problems Dwork and others saw with simple aggregation. By just aggregating data, you don't protect individuals.
But what if the dashboard didn't update as regularly, and when it did, it sometimes changed in more unpredictable ways. What if you weren't exactly sure if your screenshot was the correct number, just that it might be near the correct number, or also maybe not?
When you implement differential privacy to release a dataset or to process data, you follow several key steps:
-
Understand sensitivity: How much can a person change the result? This can be easy to measure, like it is for our salary example, or difficult to measure -- like, how much can a person's data change a machine learning model? 🤔
-
Determine bounds (if needed): Sometimes you realize that sensitivity is unbounded, meaning a person could change the result by an unlimited amount. Technically, the company could pay the person 10 billion dollars or whatever minimum wage is, so this would be a very large bound. Instead of thinking about outliers, you want to think about the true distribution and keep individual contributions within a particular bound. Choosing this bound should allow you to still do meaningful data analysis but also provide protection for outliers.
-
Apply careful noise to result: Once the sensitivity is known and the bounds are applied to the data, you can run the analysis or data processing and apply carefully calibrated noise to that process.1 Since you are essentially inserting error into the data analysis or processing2, you want to ensure that you know what type of error to adjust your analysis accordingly. For example, you might choose Gaussian noise because your dataset has a Gaussian distribution, and by applying Gaussian noise, you keep the overall Gaussian distribution intact. Differential privacy noise is tuned based on the extent of analysis and the sensitivity of the query in question, so you can to some extent decide which answers get how much noise.
-
Track budget: In differential privacy, each time you run a query you need to track the privacy impact it has on the people in the dataset. This is called a privacy budget and your budget spend is determined by parameters you set for a particular query or processing activity. Your entire budget is tracked, usually for the length of a particular analysis or process. This budget ensures that you haven't learned too much about any one individual in the group - and technically, when an individual or set of individuals run out of budget (i.e. when some limit of the parameters in that initial equation is reached), you should stop asking for more information.
I recommend reading more about differential privacy via Damien Desfontaines's blog series on differential privacy.
One graphic from his blog series shows a visual idea of how choosing different budget values (here epsilon) relate to the information an attacker can gain by analyzing the results of the data release or query:
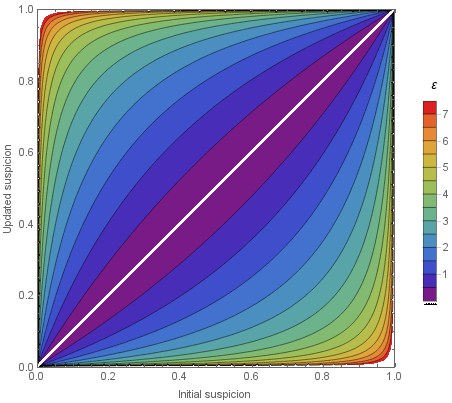 From Differential Privacy, in more detail.
From Differential Privacy, in more detail.
In this graphic, the parameter choice for epsilon is the legend. To read the graph, the x-axis shows "how sure someone is that a person is in the dataset". The y-axis shows "how much more sure an attacker will become after spending this budget". Each epsilon value has a range from the lower to the upper bound. This bound comes from the randomness chosen -- where it might be possible that someone learns more or less depending on the mechanism. However, the upper limit is a guarantee, and is what separates differential privacy from other methods.
Reading the graph, you can see that the parameter choice both affects your budget and has a fairly significant impact on the privacy guarantees. An epsilon of 5 reveals a lot of information, while an epsilon of 1 is fairly safe.
To address machine learning memorization, you could reduce the individual or singleton impact on the training process. You just need to figure out how you can apply differential privacy to something like a machine learning model. If you can do so, this provides the differential privacy guarantees for the model and for anyone used in the training dataset.3
Who has done this already? Let's investigate early research on applying differential privacy to deep learning.
PATE's Near-misses
Papernot et al. architected one of the first differentially private deep learning systems in 2017. Their architecture, called Parent Aggregation of Teacher Ensembles, or PATE, achieved high accuracy, within 3 percentage points of the baseline models.
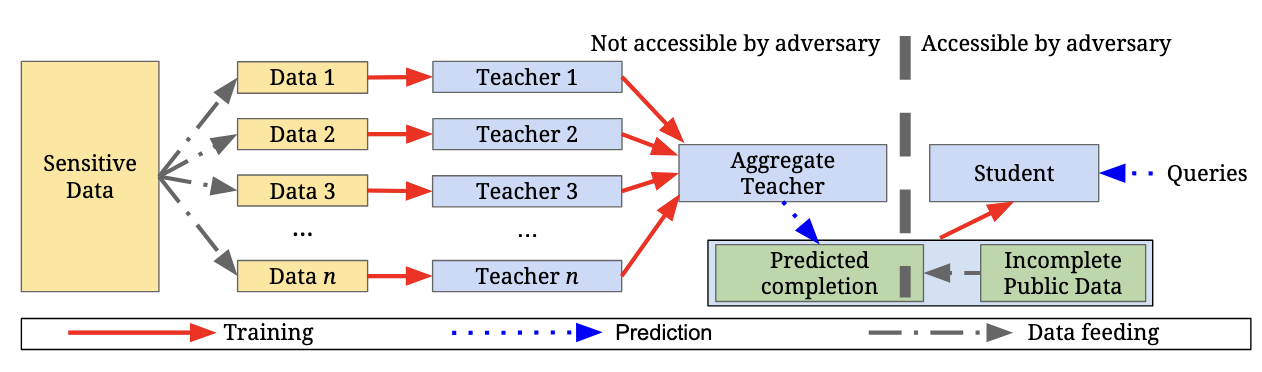
To review how PATE worked, let's review the architecture shown above. First, the data is separated into subsets so each person is only ever seen by one model. Then, many different models are trained on these datasets. After training, these models each receive one vote towards prediction or inference of a student model, which has access to publicly available data, but no labels. The votes of the trained models are output into a histogram with differential privacy noise applied and the highest class is chosen as the appropriate label. This uses differential privacy essentially as the labeling function for publicly available unlabeled data.4
In the paper, the authors found the PATE architecture "mistakes" were near-misses of odd or incorrectly labeled inputs. Here is an example from the paper, showing the correct label that PATE guessed incorrectly.

How many of these would you guess correctly? These near-misses are examples that could potentially confuse a human. In the exploration of novelty and memorization, these training examples represent uncommon or novel examples of their class. This is exactly the type of example that Feldman proved would be memorized - because not memorizing it is too expensive if you want the highest accuracy model. Using differential privacy, however, blocks this novel example memorization from happening.
Papernot et al. aren't the only ones -- much research around studying memorization have explored the link between memorization of novel examples and differentially private training.
Memorization and Differential Privacy Research
In the Secret Sharer paper, Carlini et al. compared data extraction from a model trained with no differential privacy compared with one trained using different values of epsilon.
They trained 7 models with different optimizers and epsilon values and compared the estimated exposure, which measures the memorization of a given piece of sensitive information in the language model. The paper is from 2019, so they used a recurrent neural network (RNN), another type of deep learning for language model architecture, not a transformer.
Their results were as follows:
| Optimizer | Epsilon | Test Loss | Estimated Exposure |
|---|---|---|---|
| RMSprop | 0.65 | 1.69 | 1.1 |
| RMSprop | 1.21 | 1.59 | 2.3 |
| RMSprop | 5.26 | 1.41 | 1.8 |
| RMSprop | 89 | 1.34 | 2.1 |
| RMSprop | 2x10**8 | 1.32 | 3.2 |
| RMSprop | 1x10**9 | 1.26 | 2.8 |
| SGD | inf. | 2.11 | 3.6 |
With ever increasing values of epsilon, the accuracy improves and the exposure increases. This makes sense based on what you've learned so far, because memorizing the outliers and the long tail improves test accuracy. It also shows that implementing differential privacy reduces the chance of memorizing all outliers. In this paper, the exposure and extraction attacks target outliers instead of common examples. Therefore, the exposure increases as the differential privacy guarantees decrease.
The researchers were unable to successfully perform any of the extraction attacks against the machine learning models trained with differential privacy.
At what cost? At what gain?
As you learned in the Gaming Evaluation article in this series, the present machine learning culture is focused on accuracy above all other metrics. In exploring near-misses, I hope you have begun to question this focus. Would it be okay to guess these incorrectly in exchange for better privacy guarantees and less memorization?
To some degree, differential privacy works as a regularizer for machine learning problems - forcing models to generalize and not memorize. If you want to make sure that you won't memorize any specific examples, you should apply it vigorously and as standard practice -- particularly when training large deep learning models.
The types of mistakes models with differential privacy make are small mistakes, namely reflecting the datasets' long tail. Are these mistakes worth the cost of memorizing these examples? Perhaps for generic photos, but what about for someone's artwork, voice, personal details or writing? What cost are we individually and collectively paying and how will it affect work and life years later?
Differential privacy training is not a magical salve that will solve all memorization problems for privacy in deep learning. You'll learn more about the limitations and critique of differentially private training in an upcoming article, as you begin exploring solutions to the problems discussed in these initial articles (coming in Spring 2025).
In the next article, which is also the last article focused on the problem of memorization in deep learning, you'll explore adversarial learning and examples. Adversarial learning -- similar to differential privacy research -- is an area of research that understood aspects of the memorization phenomenon long before other research caught up.
I'm very open to feedback (positive, neutral or critical), questions (there are no stupid questions!) and creative re-use of this content. If you have any of those, please share it with me! This helps keep me inspired and writing. :)
Acknowledgements: I would like to thank Damien Desfontaines for his feedback, corrections and thoughts on this article. Any mistakes, typos, inaccuracies or controversial opinions are my own.
-
I mention this because many descriptions of differential privacy mention "random noise", and that's not a very good description of what should be done. It is not uniformly random noise, but instead a noise distribution that you choose -- meaning you can fit the noise to the problem you want to solve. ↩
-
By the way, you already have error in your data because data is always an approximation and never 100% correct. For a great review on "ground truth", I recommend Kate Crawford's lecture on the topic. ↩
-
I encourage you to learn more about differential privacy, especially if you work in data science and machine learning. If you'd like to read more on differential privacy, check out Desfontaines's series and my book, which has two chapters on differential privacy and its application in machine learning. ↩
-
In theory, this system could also provide a prediction or inference service, where incoming data points are also labeled by majority differential privacy votes. Such a system was quite compute expensive to run at that time. ↩