Machine unlearning: what is it?

Machine unlearning sounds pretty cool. It is the idea that you can remove information from a trained model at will. If this was possible, you'd be able to edit out things you don't want the model to know, from criminal behavior, racialized slurs to private information. It would solve many deep learning/AI problems at once.

As unlearning is an active area of research, I've done my best to consolidate the field into three articles related to the problem of memorization.

In this article, you're going to explore unlearning definitions and clarify what unlearning is trying to achieve. In the next article, you'll study approaches to unlearning and evaluate their effectiveness. In the final unlearning article, you'll learn about successful attacks on models that have undergone unlearning. To note, all of this is part of a larger series exploring problems and solutions in machine learning memorization.

To start, what do we mean when we say unlearning? In order to build and evaluate unlearning solutions, you need to define it... so... what is unlearning?

What is unlearning?

What does it mean to unlearn something? In human speak, you might think about unlearning as simply forgetting. The interesting thing is that forgetting has been an area of deep learning study for some decades.

Usually in machine learning you are attempting to not forget! There is a phenomenon in earlier deep learning called catastrophic forgetting, where you end up with a model that has forgotten important parts of what you wanted it to learn. This happens if a model is trained on significantly different tasks and then in later training the earlier tasks are forgotten.

In the case of measuring forgetting, you can do so by looking at the error (i.e. loss) related to a particular example. This is also transferrable across model architectures, and creates a generalized way of understanding if the model has learned a particular piece of information.

Defining forgetting

Toneva et al. studied this in 2019 when investigating forgetting events. They defined these events as when an example went from properly classified to then misclassified at a later point in training.

Their motivation for studying this phenomenon was attempting to find the smallest representative dataset so that they had a minimal amount of data, but that data was enough to properly learn a task or concept. They were also curious about if these forgetting events could teach them how to unlearn anomalies or mislabeled examples/concepts.

In their research, they classified learning and forgetting by defining binary outcomes. Something is learned when it goes from being misclassified to being classified correctly and forgetting is the opposite (was classified correctly, now misclassified). Their logic could also be applied to some threshold of accuracy increase, or some threshold of ratios between true positives and false negatives, etc. Important is that there is a clear definition that can be measured of what forgetting is, and that this measurement accurately measures what you would consider adequate evidence of such an event.¹

---

NOTE

Toneva et al. measures a forgetting event in several steps:

1. Pick a subset of examples you want to study. In the paper, these are from the training dataset, but you could likely rework this metric to sample from either training or any test dataset.
2. As training progresses, track the classification or prediction result of these data points. Save these measurements in variables.
3. If there is a decrease in accurate prediction or certainty for a particular example, store the time point and the shift as a forgetting moment.
4. Continue until training is complete. At the end, analyze these events to find properties of forgetting.

---

Interestingly, they also found what they called "unforgettable examples". For them, these didn't (directly) relate to memorization, but instead were test examples that the model always got correctly once they were learned. In studying these unforgettable examples, they found that these examples were extremely generic and average. In comparison, the examples that were easiest to forget were atypical or even mislabeled.

Forgettable and Unforgettable examples in a simple computer vision model

Then they randomly selected training examples to remove and noticed that performance dropped very quickly. They were attempting to reduce the dataset size to pare down the amount of these "unforgettable" or common examples needed to still learn the concept.²

However, this approach did not work with the forgettable instances. For the ones that were valid (i.e. not mislabeled), these were key in actual learning and could not be removed without significant drops in accuracy or concept learning.³

Another interesting conclusion from the Toneva et al. paper is that the underlying data distribution complexity greatly affects the fraction of examples you can remove and still learn. They note that "for a given architecture, the higher the intrinsic dataset dimension, the larger the number of support vectors, and the fewer the number of unforgettable examples". Translated, given many of today's complex deep learning tasks, you need to have more data to learn, and that data will inform stored decision boundaries. If there are many data points supporting these boundaries, you can remove some of them and the model will still be performant. As you learned in previous articles, this also means those examples hold information on how to define those boundaries. This is also why in sparse areas, these points are often memorized.

This again proves that all datasets are not created equal! As you learned in the datasets article some datasets are massively skewed, making certain parts of the data both more valuable and more vulnerable than the rest of the data. When looking at the qualities of the data itself, it will be more difficult to unlearn complex and outlier "unforgettable" examples compared to something that is hidden in the crowd (the inverse of the sentence above, where the clustering of information from common examples provides cover -- allowing you to remove many of them and still hold information).

This has the benefit that things that aren't memorized (i.e. not "common and repeated" or "novel and class-defining") can be "unlearned" (in this definition) more easily, which is useful knowledge to build unlearning methods.

These conclusions show us:

• harder-to-learn problems require more data or result in more memorization
• some data points are more informative, making them more valuable to memorize
• forgetting is as much a property of the task and data as it is a property of the algorithms and network

If you already read the previous articles in the series you already learned some of this, but it bears repeating.

So if not all data can be forgotten the same way, and if some data must not be forgotten in order to learn properly, how can you figure out what you can safely unlearn?

What can even be unlearned? Data distributions and unlearning

If some data is inherently unforgettable, could this eventually reveal which data can be unlearned and which not? What if you need to unlearn something that is difficult or "impossible" to forget?

Tirumala et al (2022) wanted to investigate if there was a way to prevent memorization in LLMs but still fit the model with appropriate accuracy. They discovered a "forgetting baseline" which establishes a lower bounds on memorized sequences. They found that this baseline is correlated with model scale, meaning it is harder for larger models to forget things that they have learned (you already learned this in the overparameterization article).

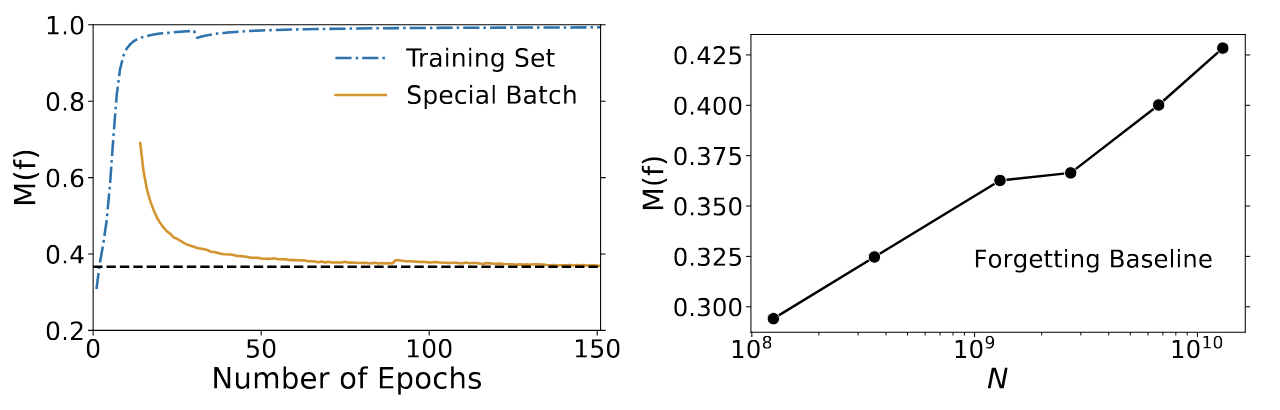Forgetting baseline increases with model size

They uncovered that there appears to be a minimum, or baseline related to model size. As model size increases, the examples that the model cannot forget increases. The first graph shows when a small batch was first learned (where the yellow graph starts). Even though this batch is no longer trained, the retention of that information continues many iterations after it is initially learned. The second graph shows this property in relation to network size (i.e. number of parameters), showing a steady increase in number of memorized sequences as model parameters increase.

To add to the complexity, Jagielski et al revealed in 2023 that repetition and task-related properties were at play. Their research determined that examples repeated multiple times are harder to forget, "more difficult" and outlier examples are harder to forget and non-convex problems create difficulties in forgetting. What does that mean?

Most deep learning problems are non-convex problems in an extremely high-dimensional space. Actually this is exactly why they do well at complex problems like computer vision, text generation, translation and multi-modal inputs (text/vision inputs combined, for example). Without these properties, you could train a simple machine learning model and have a much cheaper energy/compute bill for the same performance. Jagielski et al.'s work showed that this complexity creates difficulties in forgetting.

Forgetting relates directly to the complexity of the problem you are trying to solve. The question you need to answer: does the data you have represent the complexity of the problem space and how the model then can learn that problem space?

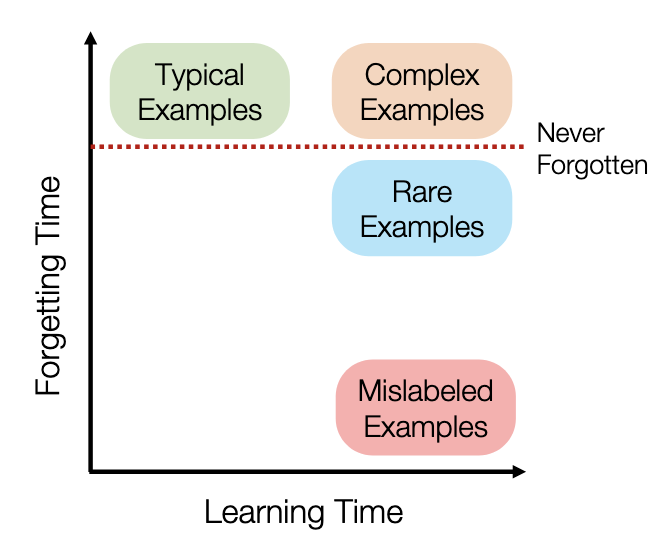Maini et al., Characterizing Datapoints via Second-Split Forgetting (2022)

Maini et al in 2022 defined these characteristics when studying forgetting in deep learning. Their research found that there was a difference in forgetting mislabeled examples, rare (i.e. infrequent but useful) examples and complex examples.

What are "complex" examples? The authors define them as "samples that are drawn from sub-groups in the dataset that require either (1) a hypothesis class of high complexity; or (2) higher sample complexity to be learnt relative to examples from the rest of the dataset."

Let's break this down by taking a short detour into exactly what complex means in this context. In this case, complex is an attribute of the amount of information you can learn in an example, compared to its peers or to the entire world of examples. If I show you something that you already know (common), you probably won't learn much unless it's your first time learning it.

This complexity can also relate to the class itself, where the class is in-and-of-itself an unexpected or surprise occurrence (i.e. an anomaly or aberrance). This "surprise" element can sometimes (but not always) be synonymous with what is meant by "outlier" in a distribution.

The neat thing is that this complexity has been studied for almost as long as computers have existed. Essentially, this complexity represents what Claude Shannon called information. Shannon's information theory explains how complex data holds more information.

This theory is the basis of much of computational learning theory, where you want to extract information and store it in another format (a model, for example) that can hold this information in a compacted and compressed way for future use. As you can imagine, some information is more complex and useful than other information -- ideally you are only storing and communicating the most essential information when you want to learn or communicate efficiently.

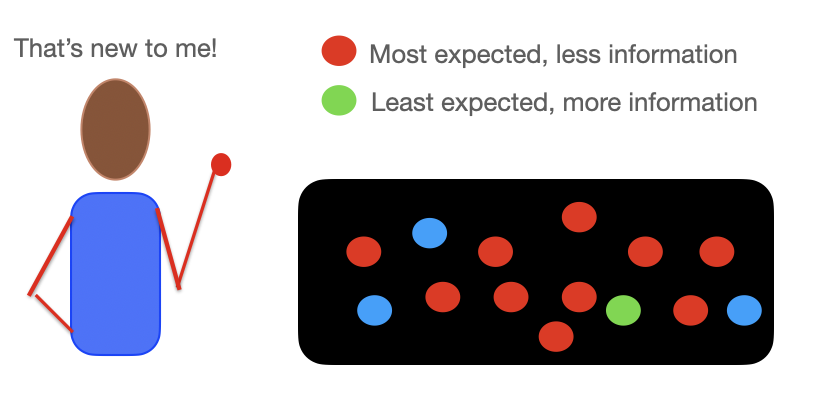
To better understand how information theory and learning theory work together -- imagine you are pulling different colored balls from a jar. After a few pulls of only red balls, you start to expect to see more red balls, maybe there are only red balls in there? Then you see a surprise blue ball. This ball holds more information, which helps you learn. This "aha!" is one example of both information and a "more complex" outcome -- which is what you are trying to store in your model, so the model is also not "surprised"⁴ to occasionally see a blue or green ball, even if it learns the majority are red.

Essentially this is the goal of today's deep learning systems when you want to learn a "world problem" and save it in a multi-billion/trillion parameter model (which is in the end able to be compressed into several very large files on a computer). You want this model to have held all of the information needed to take an input and give a useful, informative output based on every piece of that information (and potential links/signals learned from these "surprise" connections based in information theory).

Unfortunately there isn't a universal way to measure information in a piece of data, especially if its complexity (and therefore information content) is relative to the learning problem or to the dataset (or world!). You can, however, use the learning process to recognize more complexity, because these classes/examples/problems will probably take longer to learn and demonstrate stronger memorization properties when compared with less complex examples or classes.

Perhaps these data points can teach us something about recognizing memorization and forgetting. In all of the papers you've explored thus far, there are different metrics the authors use to define this phenomenon. Maybe studying and better defining forgetting and learning can help you establish a baseline for example complexity and frequency within a population. This, of course, must account for things like model size and problem complexity.

Most currently-developed ways of studying this problem are applied late in the learning process, via a modified training (i.e. leave-one-out) or after the model has been trained. You would need to fundamentally shift the machine learning training and evaluation to evaluate these properties during normal training, so that there can be appropriate metrics which are also efficient and scalable. As of yet, there isn't a universal definition or standard for doing this, and the research around how to appropriately measure this is not designed to scale and certainly isn't yet built into machine learning frameworks.

With that in mind, you still need to define unlearning -- especially in relation to memorized / "unforgettable" examples. Going back to a metric that is easier to measure, you might remember Nasr et al's work on defining memorization as to whether it is discoverable or extractable. This relates back to our two attack definitions. Perhaps these can lead us to a clearer definition, one that is both measurable and scalable.

I swear I didn't see it: Model-based definitions

Putting the focus back to the model itself, perhaps there is a definition that looks at the model behavior, fidelity or other properties to define forgetting and/or "unlearning".

As you learned from a previous article, one way to differentiate between memorized examples and not memorized examples is to use the leave-one-out training to develop several models and then compare a model that has never seen a training example with one that has. But is there a way to determine that a model behaves similarly without having to train hundreds of large models?

Some unlearning approaches look at measuring the distance between models. However, because many neural networks can learn the same task or same functions with random initialization weights (especially ones with millions of parameters), the similarity or distance of the weights of a network is not a very good choice for evaluating model similarity. It's easy due to permutation invariance (a cool property of linear algebra) to have different weights and yet the same outcomes.

In 2023, NeurIPS ran an "unlearning challenge", which attempted to define unlearning. The measurements used in the challenge were predominantly defined and then evaluated by Google researchers, and included several interesting qualities:

• They choose "average case" datasets, where the worst-case scenario of unlearning only complex examples is removed.
• They use the definition of differential privacy to define a new unlearning measurement that is weaker than the concept of differential privacy, but that they claim is sufficient for proving unlearning.
• This definition attempts to keep model predictions between a model that has never seen the data (leave-one-out) and the model that has undergone unlearning close. Both models should behave as similarly as possible.

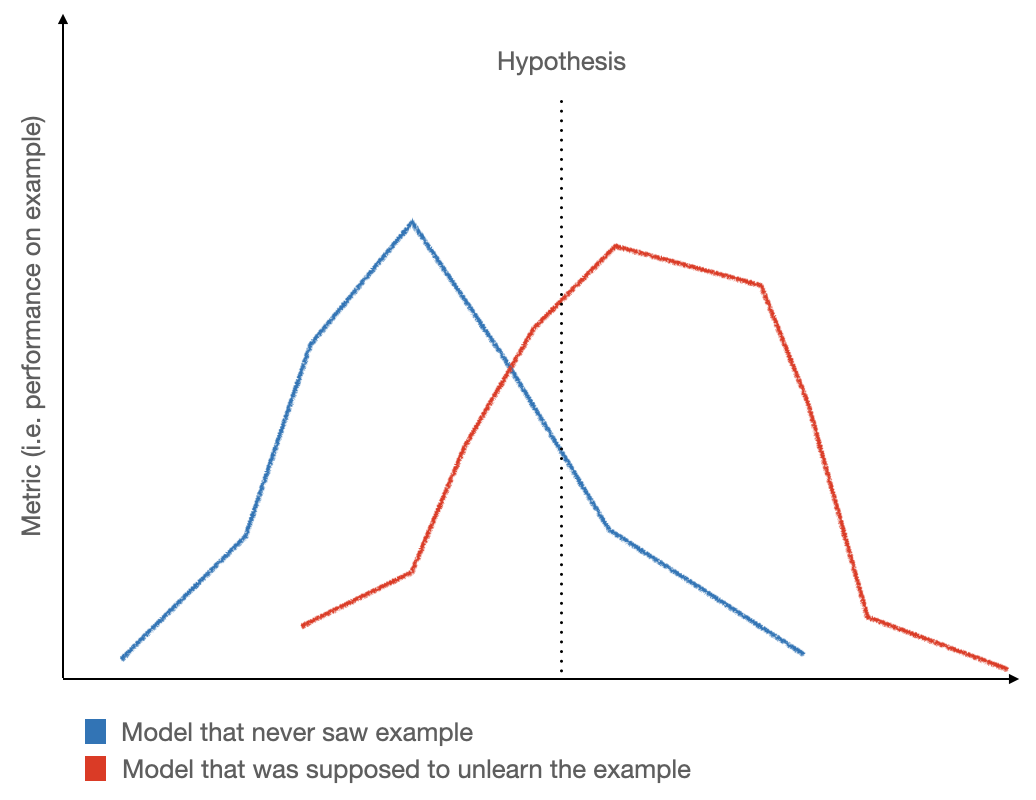
To visualize this challenge and the measurement, you compare the leave-one-out model prediction performance metrics across an example set to that of the unlearned model. Similar to differential privacy attacks, the attacker must try to differentiate between the two models. The attacker only has query access to "some model" and must decide if that model is the one that has never seen the data or the one that has unlearned the data. Of course, if you have both models you can simply test both across a sampled subset and determine if this attack would be successful.

As you have learned from the memorization series thus far, a model that has memorized a useful complex example or even a less useful common but repeated example will score higher on similar examples than models that haven't seen this information before. Therefore, this unlearning metric attempts to exploit this and see if there are examples that demonstrate the difference between the models.

Similar to the attacks defined, this attack works best by finding a likelihood ratio exploiting several accuracy dimensions (False Positive Rate and False Negative Rate). The attacker can bring any prior knowledge they have to create an initial assumption and then query the "unknown model" many times in order to update their suspicion on if that model has changed (i.e. if the unlearned and other model behave differently).

When doing so, an intelligent attacker would keep a history of all the queries and begin to distinguish minor differences by looking at the distribution of responses overall. Eventually, they might find a worst-case scenario query that clearly shows them how the query responses are easily separable.

In the metrics definitions for the challenge (PDF), the authors use two attacks to measure the unlearning quality of the models. They then choose the best result for a particular example to calculate an epsilon that measures the divergence between the two models. They do this for the sampled subset that represents the forget set examples. Then, they average these epsilons across all their successful attacks or best guesses to determine what they call the "forgetting quality" of the unlearning approach.⁵

You'll evaluate the approaches for the top scorers in the next article, but remember that this entire measurement requires a predefined forget and retain set and the ability to measure and compare the approach with a leave-one-out model. Presumably the authors could also say that the best approaches automatically extend to other models and therefore you do not need to measure every time -- but because you know that model architecture and datasets greatly influence memorization, it would be difficult to argue that one sandboxed experiment demonstrates a universal approach.

Privacy-attack metrics as a measurement

In the end, this unlearning metric greatly relies on privacy attacks as a measurement. These attack metrics can also be just directly used to determine the exposure of a given example or set of examples or even across the entire training dataset.

For the challenge, the attacks and tools used were inspired directly by membership inference attacks, such as LiRA. On Google's post about the challenge, they state:

Intuitively, if unlearning is successful, the unlearned model contains no traces of the forgotten examples, causing MIAs to fail: the attacker would be unable to infer that the forget set was, in fact, part of the original training set.

So why not just use these attacks as the gold standard? Although they do require extra compute and time to evaluate models, they clearly help model developers and engineers better understand and address the concerns raised by memorization. New attacks should be developed and researched in case there are better ways, but practitioners need standard definitions to allow for comparison and evaluation.

Additionally, LiRA and extraction attacks could be standardized and integrated into normal machine learning evaluation pipelines -- allowing data scientists and machine learning engineers to evaluate the effectiveness of their interventions and track memorization "metrics" in their systems.

Of course, with LiRA you need to decide how to hold the attack at a reasonable "true positive rate", so you are accurately guessing which data the model has seen and which not. In addition, there will always be "worst case" versus "average case" debates about which is adequate to properly define unlearning. Much of this could standardize over time in scientific literature as the field matures and as legal and privacy scholars become informed enough about the distinctions to offer advice.

Even if you weaken the definition to some average case scenario, you can imagine a way where you might not actually prove you didn't learn a thing, you might simply hide that you learned it. You can think of this as a slight remodel -- the walls are still there but they are a new color, can you find the artifacts that remain?

Harry who? Approximate unlearning

If you don't want to use a precise measurement, you can perhaps find an approximate measurement. This is exactly what Microsoft Research investigated in their research Who's Harry Potter? Approximate Unlearning in LLMs.

They studied how they might be able to unlearn Harry Potter as a concept. They didn't want to necessarily prove they never learned Harry Potter (MIA) or even never mention the name. They just wanted to make sure they didn't do it often or consistently.

In this "approximate" unlearning, they encountered other problems with picking a famous person-like character:

1. Related concepts: There are several persons related to Harry Potter, like Ron and Hermione. How do you just remove Harry without also eliminating other persons in Harry's proximity?

2. Downweighting the correct embeddings: Making it hard to answer "My name is Harry" also deprioritizes the token sequence "My name is", which is not what you want to do.

3. Disambiguation: There is more than one Harry! How do you remove the correct one?

4. Unlearning the correct links: How do you maintain links to other concepts, like Magic and Hogwarts while delinking Harry?

5. Simple replacements are too simple: Simply replacing tokens (i.e. substitute a new name "John" for Harry) leads to concept confusion, like the LLM responding with two persons acting as one. "John found his keys and then Harry left the house."

To deal with these issues, they replaced several core concepts with more "generic" concepts. They then fine-tuned the model to "relearn" these generic links, suppressing the Harry Potter likelihood via this additional training.

After that additional training, they reached a result where they determined the slippage was appropriate (i.e. Harry was rarely mentioned). The authors note that Harry Potter and linked concepts exist in their own universe, which allowed this to be more easily extracted from information in other concepts.⁶ Non-fiction content and real humans could be more difficult to remove.

Open Problem: Lack of clear definitions

As you have learned thus far in this article, there are many differing measurements, metrics and ideas about what "unlearning" or "forgetting" could mean. Because there isn't yet a clear, agreed-upon definition of unlearning it is also a difficult field to effectively contribute to, because how can you move the needle on a problem when you haven't yet defined the problem?

From the Google Unforgetting challenge:

The evaluation of forgetting algorithms in the literature has so far been highly inconsistent. While some works report the classification accuracy on the samples to unlearn, others report distance to the fully retrained model, and yet others use the error rate of membership inference attacks as a metric for forgetting quality.

Since you might want to compare 10 different approaches to unlearning, you are then trying to evaluate them with 3-4 different types of measurements. How do you choose the best one for your data and use case? Do you have time to evaluate every approach? Where is the advice on how to fix your specific unlearning problem?

To make things more complicated, when lawyers or policy experts look at these problems, they see a myriad of other issues. Research from a multidisciplinary team of researchers in big tech and universities pointed out that being able to unlearn one particular artist doesn't remove their influence on a group (i.e. Monet and the Impressionists). Being able to remove all pictures of Batman doesn't remove all references to the idea of that superhero, and even all photos of someone cosplaying that character. Essentially their advice focuses heavily on copyright and advises that you use guardrails to attempt to block violations, but they present a sound discussion of the complexity of the issue. Since there isn't yet much legal guidance, defining unlearning, both technically and legally, is going to be a long process.

Additionally, it's hard to disentangle concepts in data at scale. Thudi et al. called for better auditable unlearning definitions, noting that it's easy to learn the same information from a different data point. This is similar to the problem with graph networks, where if you delete your data, it doesn't mean that a friend of yours isn't sharing your data without your permission (i.e. via their contact book or an uploaded photo). Without a clear definition that is both auditable and that reflects the societal and personal views of privacy, it's problematic to call unlearning "done" or even achievable.

Taking a personal and social view of privacy, your data might be easily traceable but you as a concept are not. Other people can contribute data about you without your consent because that's how data works -- it's unlikely that you'll ever have a full view of what digital data about you exists. That said, creating a better conversation around what humans want and what is technically sound could help create an understandable, feasible and auditable definition.

To be clear, that's a big part of why I've been writing this series -- to hopefully spark conversations and insights across disciplines in order to help guide better, clearer, safer definitions of Privacy-by-Design AI systems.

Unfortunately I won't wrap up this post with an answer to this question, but I hope I've sparked some thinking around how to talk about the definitions currently available and begin to reason about which ones resonate with you, with your team, with your legal or policy expertise and with your own data.

In the next article, you'll be exploring different ways researchers and teams have technically approached unlearning. You'll dive deeper into the problems of unlearning critical information. You'll also look at other open problems in unlearning, like scaling unlearning for real-world problems.

As always, I'm very open to feedback (positive, neutral or critical), questions (there are no stupid questions!) and creative re-use of this content. If you have any of those, please share it with me! This helps keep me inspired and writing. :)